Wavelength

Sounds, pure tones and sinusoids.

Most musical sounds contain a complex mixture of frequencies. Hence, the spectrum of music usually has a wide range. But for measurements and theoretical considerations we often look at so-called pure tones, which consist only of one single frequency.

If we look at such a single-frequency signal’s waveform, it looks like a perfect sinusoid.
While for example singing a single note produces a wide range of frequencies, an easy way to create a good approximation of a pure tone is by whistling.
Try and check your skills with one of many realtime analyzer apps on your phone!
(Realtime analyzers show the spectrum of their input signal along a horizontal frequency axis. A single frequency should show only one vertical line, but because of limited frequency resolution it might also raise two adjacent lines.)

Since many acoustical phenomena are frequency dependent, it is often easier to describe them at fixed frequencies.

Launching a wave

Let us assume a loudspeaker that radiates on cycle of a pure tone. In the process, the loudspeaker cone excursion follows the shape of one sinusoidal cycle:

Initially, the cone starts to move forward and thereby locally produces increased air pressure in front of it. Of course, the air will expand forward to relieve this pressure, in the shape of a wave that radiates from the loudspeaker cone and expands forward with the speed of sound.

After one quarter of the single cycle movement, the cone has reached the sinusoid’s maximum: It starts to move back, „inhaling“ air and thereby produces a negative local pressure change. After another quarter it passes the rest position. Another quarter later it reaches the negative sinusoidal peak, and from there returns to the rest position where the full cycle is finished.

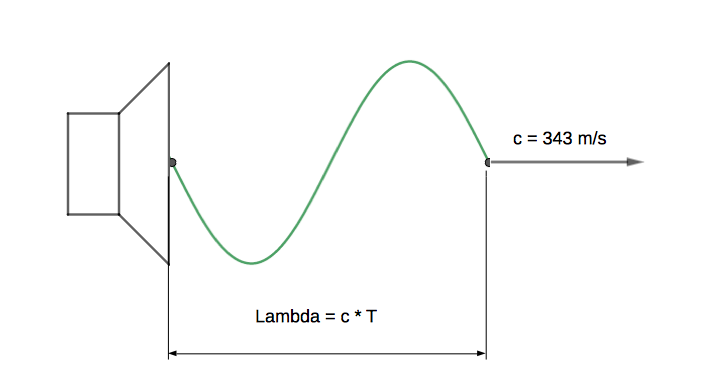
Wavelength Lambda

Let us now freeze time and look at the pressure distribution in front of the cone:

The initial wavefront has spread out, with sonic velocity, from the loudspeaker cone forward: To a distance „Lambda“ that equals the product of that velocity „c“, and the duration “T“ of one sinusoidal cycle.

Lambda = c * T

c, the velocity of sound, is about 343 m/s.

Summarized, wavelength Lambda is the distance covered by the sound during one cycle of it’s frequency.

The periodic time T (seconds per cycle) is the inverse of frequency f (cycles per second, or Hertz):

T = 1 / f

The resulting formula describes the relationship between frequency and wavelength:

Lambda = c / f

Therefore the wavelengths corresponding to our hearing cover a wide range from about 21 m @ 16 Hz to only 17 mm @ 20 kHz.

Since the effect of objects on the propagation of sound usually depends on the proportion of object size and wavelength, it is now easy to understand that it takes large objects to influence low frequencies.

Let us keep this in mind for further discussions.

Final comment:

Experts, please mind that as mentioned before (Acoustics-introduction) I try to use simplified terms and analogies, hoping to illustrate an invisible pressure distribution. Hence, details like radiation impedance and the phase relationship between pressure and velocity are neglected. Nevertheless, understanding wavelength will help to understand radiation impedance …