Modal coupling – aka Low Frequency Optimization
Modal coupling is about how your loudspeaker’s and listening position influence the reproduction of low frequencies (LF) in your room.
Fundamental frequencies
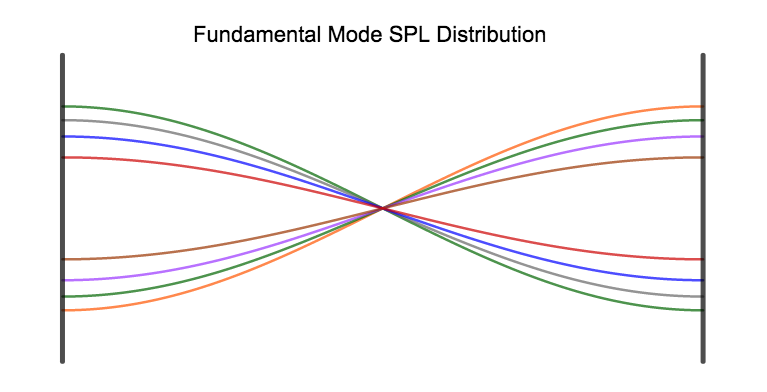
We have been talking about room modes in the resonance blog. At a resonant frequency, eg. between two hard, parallel walls, a fully excited room mode produces a standing wave pattern. For the fundamental resonance, the sound pressure level (SPL) is distributed as shown above. There is no pressure in the middle between, and high pressure directly at the walls. At high SPL points instantaneous pressure changes during the cycle of the frequency, but at zero pressure points of the mode there will never be pressure.
Two parameters influence the modal coupling: the loudspeaker position, and the listening (or measurement) position.
We fully couple a loudspeaker to a mode if we place it at points with high SPL, and decouple it from the mode by placing it into a „null“. And the same happens with our listening position: if the loudspeaker excites the mode, we will hear it (or measure SPL) at the high SPL points of the standing wave pattern, with nearly no sound at the „nulls“.
But there are more than just the fundamental frequencies resonating in your room
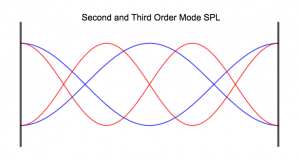
As discussed in the resonance blog, there are higher order modes as well. Due to their smaller wavelengths, their standing wave pattern is denser. High SPL zones and nulls are closer together, and there is more than one null between the walls.
It is a 3-D world
Finally, in a rectangular room there are 3 fundamental frequencies between the parallel boundaries. In addition to these axial modes, there are tangential and oblique modes. And all these resonant paths have higher order modes, as well.
IF the walls are rigid, and IF the room is rectangular and empty, the modal pattern can be calculated for all modes.
But in reality there are flexing boundaries (drywalls tend to resonate around 100 Hz, windows at even lower frequencies). This shifts the effective reflexion points outwards of the physical size of the room.
Also, there are rooms of more irregular shape.
To precisely calculate these influences the so-called Helmholtz equation that describes the modal behaviour needs to be solved. This is usually performed with numerical approximations like finite element analysis (FEM) or boundary element analysis (BEM) software. Time consuming and expensive, and also depending on the precision of the model description. Do you really know the compliance of all your walls? The absorption and damping characteristics? And of the furniture?
I assume, you will not be positively excited if I recommend to solve bass frequency problems with such calculation.
Some real world scenarios
Some dominant modal problems can often be found in real world listening situations:
Example no 1: Small speakers placed on some furniture approximately at half room height.
Let’s calculate the fundamental for a room height of 2.5 meters: half wavelength equals room height, therefore the fundamental frequency has 5 m wavelength. That is 343 / 5 = 68.6 Hz, which will be strongly be reduced in SPL due to this placement.
Even worse, if sitting, we mostly have our ears around 1 – 1.3 m height. This is again just in the middle of such rooms height. Hence attenuating SPL at 65 – 70 Hz again!
Therefore, even if they are now located below ear level, place such small loudspeakers on stands or furniture of lower height. Adjust vertical tilt according to the radiation characteristics, typically with the tweeter directed to your ears.
Example no 2:
A dedicated listening room. Left and right loudspeaker are placed symmetrically, for best stereo reproduction. And the listening position is in the middle between left and right sidewall.
With both speakers placed at the same modal pattern points between front and back wall, this direction produces the strongest resonance pattern. At for example 5 m room length the fundamental is 34.3 Hz. Sitting close to the middle of the room will suppress the lowest end just as much as placing the speakers there. Careful choice of listening and speaker position within the standing wave pattern will balance things nicely.
Don’t forget to consider the influence at the second order room mode around 69 Hz in similar ways!
Example no 3:
Just like no 2, let us assume major problem solved by careful symmetric setup as outlined above.
So, all other room modes are coupled into by the speakers and received by the listener in symmetrical fashion.
Therefore, if the room is „problematic“ (worst case may be hard basement walls, quadratic floor shape, and semi-cubic height), even higher than second order modes will ring terribly. Of course, some acoustic treatment is unavoidable here. But as a first aid, we can decide for an asymmetric setup. Here, left and right loudspeaker are placed with their symmetry axis (towards the „sweet spot“) shifted towards a room diagonale. So that they end up coupling into room modes differently. Since the lowest frequencies are often recorded in mono, this asymmetric setup helps to balance room mode excitation a bit.
Hint: even if we are talking about long wavelengths, often movements of less than 10 cm can have strong influence on LF SPL.
Example no 4:
If you happen to listen with multiple subwoofers, and have 4 or more in use, you already may know the following: Placing them about center close to all 4 walls on the floor around you may produce a nice, flat balance within a wide listening zone. Usually for the lowest 1.5 octaves. If you didn’t know and have the stuff at hand, have fun trying and figuring out how this works.