Loudspeaker Phase Response
![]() Text to speech – TestHiFi Blog: Loudspeaker Phase Response
Text to speech – TestHiFi Blog: Loudspeaker Phase Response
Loudspeakers usually radiate different frequencies with different phase. This is due to the drivers themselves, interaction with the cabinet, and the crossover.
A basic example of phase lag would be the inertia of a woofer due to it’s moving mass. With increasing frequency the excursion lags behind the driving signal, reducing output like a low-pass filter. Actually, all those cones and domes in our hifi speakers are 4th order bandpass devices by themselves. Their output rises with second order steepness (12 dB / octave) from DC towards their fundamental resonance (eg 40 Hz for a modern 2-way woofer). And drops again with about second order steepness above 2-3 kHz (beaming may reduce this on-axis). Crossover and cabinet influence usually increase these effects.
In my Blog about interference I tried to explain how waves of the same frequency add up depending on relative phase. Perfectly in phase they will sum to twice the amplitude, or +6 dB. 180 degrees phase shift will cancel them out.
A phase shift of 90 degrees leads to a summed signal of +3 dB (doubled power, see top picture).
Most hifi loudspeakers use different drivers for high and low frequencies. A crossover network is used to smoothly hand over from the low/mid frequency unit to the tweeter.
The slopes of that crossover determine the phase response of the loudspeaker at the crossover frequency. Steeper slopes introduce larger phase changes.
The magic „impulse perfect“ first order crossover
SPL behaviour is shown below.
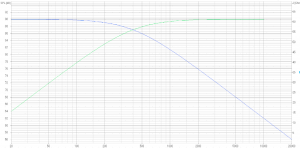
1st order SPL
I choose a crossover frequency of 400 Hz. The woofer (LF, blue) and mid/tweeter (HF, green) output is 3 dB down at that frequency to add up to a linear overall response. This is due to a 90 degree phase difference between LF and HF. Would they be perfectly in phase, their combined output would sum to +6 dB at 400 Hz. See the phase response below.
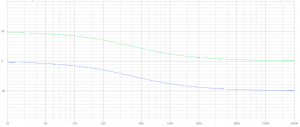
1st order phase
The result is that while on-axis the response of such speaker is flat, it will have a (downward) lobe with higher output than on-axis. Not good.
At the crossover frequency, the LF driver lags 45 degrees, while the HF system leads another 45 degrees. With the hand-over from woofer to tweeter, there is a gradual phase change from the lagging LF to the leading HF. In an ideal world this would keep the total phase about constant with frequency. Around the crossover, we have both systems running with similar SPL, radiating with 90 degrees phase difference.
Second order filters
Same now with so-called second order filtering, at 12 dB / octave steepness.
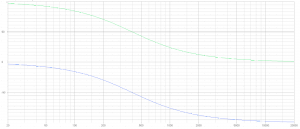
SPL with both drivers connected in phase
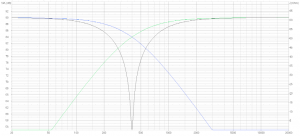
2nd order in phase SPL
Phase response
2nd order connected in phase
Due to a 180 degree phase shift between LF and HF they cancel out around the crossover frequency.
Easy solution: invert the phase of one driver (HF choosen) and they sum up perfectly.
SPL with inversion
2nd order rev connection SPL
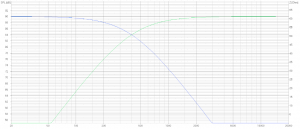
Phase response is the same for LF and HF, but with HF leading one half cycle plus inversion. You cannot see this in below phase plot because of the wrapped-around-180-degree phase.
2nd order reverse connection phase
Fourth order filtering, with 24 dB / octave slopes
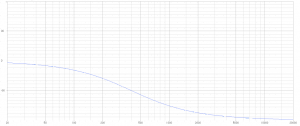
You can see the steep slopes in the SPL plot of both drivers. Their combined output is well in phase and adds up to 6 dB at the crossover frequency. But LF lags 360 degrees behind HF now, a whole cycle! Which you don’t see in the phase plot, which wraps around +- 180 degrees in my graph.
4th order SPL
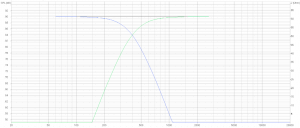
Within a very short frequency interval the dominant SPL output is handed over from LF to HF. Within the same interval around 400 Hz the dominant output’s phase changes 360 degrees. HF radiates one cycle earlier than LF.
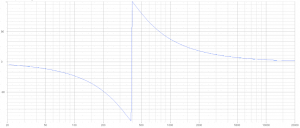
4th order phase
Crossover time delay
Acoustically there is no difference in phase shift whether the filtering results from cone mass, driver voice coil inductance or active / passiv filters.
At the crossover frequency, LF is radiated with a phase delay of 90 degree behind the tweeter for 1st order filters. For 400 Hz that would be a delay of one-quarter cycle, or 1/(4*400) = 0.625 ms.
The 180 degree phase shift of a 2nd order filter introduces 180 degree LF phase lag compared to the tweeter output, which will therefore lead a 400 Hz pulse by 1,25 ms.
And, the polarity of one driver needs to be inverted.
Finally, today’s most popular crossover seems to be 4th order. LF is one whole cycle behind HF at 400 Hz, radiating 2.5 ms later.