Resonance, standing waves and room modes
Room modes
Resonance happens in systems that can oscillate. Rooms are such systems,
and their resonances are called room modes. Loudspeakers excite these room modes more or less depending on their position, creating so-called standing waves.
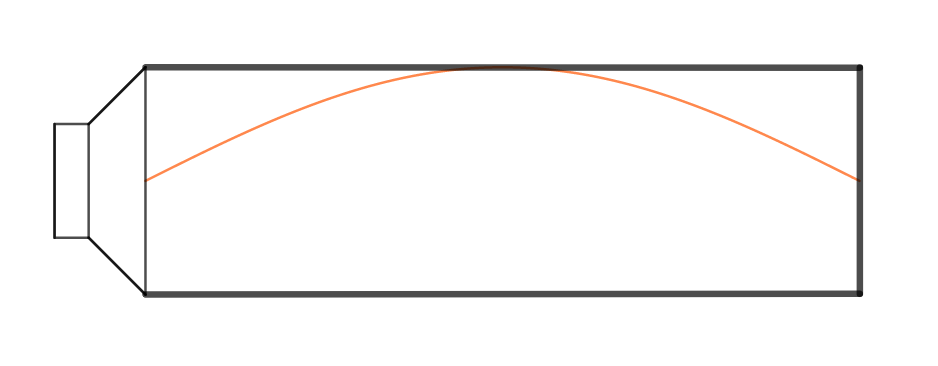
We excite a room mode most intensively if we place a loudspeaker close to one of two parallel walls. Now there is a similarty to a pendulum or a playground swing. Pushing a cone, pendulum or swing forward in sync with its natural frequency increases the energy with every cycle, up to huge amplitudes.
This condition is met if the wavelength radiated is twice as long as the distance between the parallel walls. In other words, that distance equals half-wavelength. Example: wall distance 5 m, fundamental room mode perpendicular to those walls at 10 m wavelength or 34 Hz.
The SPL gain of a fully excited room mode may be 30 dB or more, in typical listening situations you usually can observe 10-20 dB. A 20 dB gain is equivalent to 100 times more energy!
Resonance also occurs at frequencies with wavelengths that are multiples of the fundamental described above. Their reflection from the opposite end reaches the loudspeaker in sync with its own movement. Hence, our above example produces higher order modes near 68, 102, 136 etc. Hz.
closed end tube modes
Tube resonance
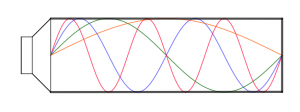
The same kind of resonance happens in a tube with both ends closed. Interestingly, a tube can resonate also with one end open!
How this works seems less obvious …
Imagine the loudspeaker sending the negative half of a cycle into the tube. Let the frequency’s wavelength be 4 times the lenght of the tube. This creates a negative pressure wave with appropriate frequency, that reaches the open end after a quarter of it’s wavelength. Now that we have a lower pressure level inside than outside at that open end, air rushes in from outside. This inrush creates a pressure wave running back into the tube. The negative pressure is reflected into positive pressure at the open end. After another quarter cycle it reaches the loudspeaker cone, in sync with the loudspeakers next pressure cycle. Every half cycle of cone vibration the inverse reflection at the open end increases the energy of this standing wave.
For a tube of 5 m length the fundamental resonance (tubelength equals quarter-wavelength) occurs around 17 Hz. Try to form a tube with your hands in front of your mouth and talk through it: Length is around 10 cm, fundamental resonance 860 Hz. This frequency will be boosted by your improvised tube.
open end tube
Position dependancy
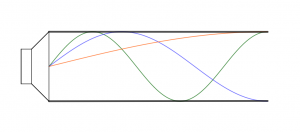
Now, let us examine what happens if we move the loudspeaker from one wall to the middle of a standing wave at the fundamental frequency. The loudspeaker starts a cycle by sending a pressure pulse in both directions. That positive pressure wave reflects back from both walls at the same time. It reaches the loudspeaker after one-half cycle, just when it starts to create the negative pressure part of the cycle. The reflected positive pressure wave cancels the negative cycle.
Therefore, a room mode enhances or supresses the loudspeaker output, depending on the speaker placement with regard to the standing wave pattern.
The same happens with higher order modes (multiples of the fundamental) and the placement of the loudspeaker relative to their wave-pattern. With a difference: the fundamental increases energy with every cycle enhanced by the loudspeaker.
Moving up the frequency scale one octave higher enhances the next room mode only every second cycle.
Therefore the modes influence at this frequency will be less than at the fundamental.
The higher a room modes order, the lower it’s influence on the loudspeaker response.
Experts, please mind that as before I simplify things hoping to provide an easy to understand model of the physics involved. No velocity or gradient sources, no phase relationships, damping and vortex effects etc.
Another important acoustic resonator is the Helmholtz resonator, which is more complex to understand. Subject for a future blog.