Woofer Size
Why woofers need to be large to radiate efficiently
Due to a recent discussion about efficiency and directivity:
Is higher efficiency – like with horn systems – a result of
higher directivity? Produced by restricting sound energy
within a smaller radiation angle?
My answer would be yes … and no.
A simple comparison
Most of us know from experience that swimming with fins is more efficient
than bare foot. In similar ways, a large woofer cone compresses air more
efficiently than a small one.
As a model of thinking towards „why“, I offer the following:
Imagine to be an air particle.
Suddenly a large, heavy object moves towards you, obviously wanting to push you.
You could now try to escape by accelerating to a speed faster than the object,
but doesn’t that seem to be more effort than stepping sideways?
If the object isn’t too large. Which depends on how fast you can move.
Let us assume you could maximally move with the speed of sound.
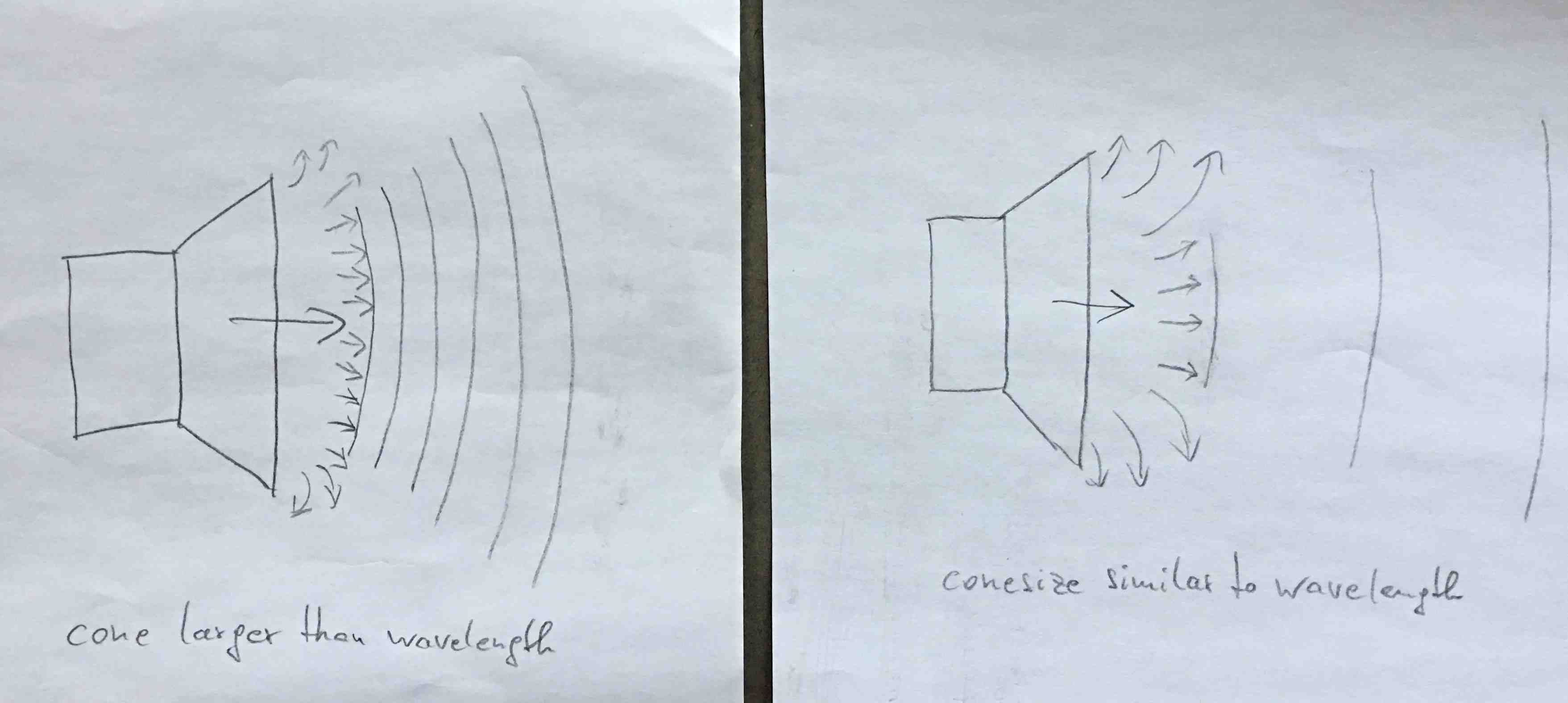
Smart moves in front of a rigid piston (cone)
In our case the object is a rigid piston.
It moves harmonically at some low frequency (LF), with cycle duration „T“.
The forward movement of the positive pressure stroke
lasts one quarter cycle „T/4“.
If you are close to the edge of the piston, and the radial escape
route within „T/4“ can be made at a speed lower than the average
piston movement, that route makes sense.
The other extreme would be right in the piston’s center.
To reach the edge within „T/4“ with speed of sound „c“,
the piston radius needs to be smaller than c * T / 4.
c * T = wavelength L of the frequency f radiated.
(The distance sound travels within one cycle)
Can you move far enough – fast enough?
If the piston radius is much larger than a quarter wavelength,
it will pressurize the air easily.
If the piston radius is much smaller than the quarter wavelength,
the air will move more sideways than in the direction of the stroke,
and little pressure will be generated.
If we now increase the frequency, the wavelength gets smaller
compared to the piston radius. Radiation gets more efficient.
The relation between pressure generated and piston movement
is described by …
Acoustic impedance
So this is not a constant resistance of the air against the piston move,
but a more „complex“ impedance, varying with frequency.
Acoustic impedance raises with frequency, towards a point where
piston diameter is about half wavelength.
Or, as used above, piston radius is about c * T / 4.
Above this frequency „F“, acoustical impedance is, besides a few wiggles,
relatively constant. All in all it looks similar to a second order highpass.
Yes, I know – this is a VERY simple description,
mixing particle velocity with speed of sound etc.
But it avoids Laplace operators and differential equations.
Does this help to understand why large woofers radiate LF more efficiently?
And why constricting sideways movement in front of a driver
via a horn is another way of increasing efficiency?
And no, this has nothing to do with beaming.
Rigid piston beaming starts around – again – that frequency F where
cone diameter equals half wavelength (for a nominal 8 inch woofer …
above around 1 kHz). Which is the range where acoustic impedance is
nearly constant.