Acoustic radiation impedance

What is radiation impedance? Let us have a look at Wikipedia:
“Acoustic impedance and specific acoustic impedance are measures of the opposition that a system presents to the acoustic flow resulting of an acoustic pressure applied to the system.”
(https://en.wikipedia.org/wiki/Acoustic_impedance)

I try to simplify this to our needs: A simplified term for impedance is resistance. Radiation impedance is the resistance a diaphragm sees when it moves air to create a soundwave. It creates sound pressure and feels this pressure as opposed to it’s movement.

Loudspeaker efficiency and radiation impedance

Regular hifi loudspeakers produce sound energy with an average efficiency between 0.1 and 1 percent.
Do you know why the efficiency of loudspeakers is so low?
Because for low frequencies, the radiation impedance – which describes how much pressure the diaphragm creates by it’s movement – is very low.
For higher frequencies radiation impedance raises, but due to the inertia of the diaphragm mass the movement’s amplitude decreases at similar rate. Therefore, sound pressure is created at near constant low efficiency above most of the usuable bandwidth of our speaker.

Why is radiation impedance so low?

For the simplest explanation I can offer please remember the postings about wavelength and diffraction.

Imagine a small loudspeaker cone moving slowly while producing a very low frequency wave. The air in front of it flows easily aside, instead of being pressurized.
But if we increase the cone diameter, the air will need to accelerate aside faster. That means, there will be more pressure buildup in front of the cone, equivalent to more impedance – and efficiency.
As soon as the diameter gets larger than one-half wavelength of the frequency under consideration, the sideways-pressure release will not be fast enough: A strong pressure wave is radiated forward.
From the start of one sinusiodal cycle, there is one quarter of the signal period’s time to “escape” until maximum cone excursion is reached. During this time the air (or more precise, the pressure wave) can move one quarter wavelength.
The air near the cone’s circumferance will always easily evade. But those particles near the cone center will be set under pressure before they can release this pressure sideways. Before this expansion has reached the edge of the cone, the cone starts to move backwards, lowering pressure again.
Hence, the cone’s radiation impedance will raise with frequency until one-half wavelength equals cone diameter.

Can we improve radiation impedance?

As above, similar to swimming with and without fins large diaphragms work with higher radiation impedance and efficiency than small ones.

But there is another way to prevent the sideway “escape” of the air:
Put a funnel in front. We all know how to fold our hands in front of the mouth to call out louder. The same happens to a loudspeaker diaphragm mounted on a horn.

1 + 1 = 4

Another alternative is to use multiple drivers close to one another. We start with one 8 inch woofer and look at it’s low frequency response, at 1 W input and 1 m distance (black line). Diameter = 16 cm, half wavelength at 1.050 Hz.
Now we add a second one directly beneath the first one, again with 1 W input – total input power is now 2 W (red line).
Sound pressure level (dB) to the left, radiation impedance right:

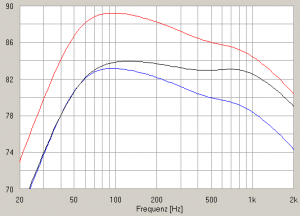
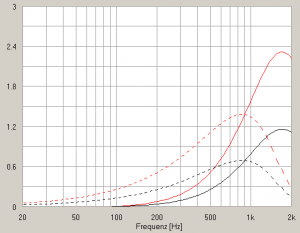
The gain is 6 dB, versa an input power gain of 3 dB (doubling of power).
Doubling the transducer area has doubled acoustic impedance and efficiency.

The blue line represents 2 woofers but with power reduced to achieve similar low frequency (below 60 Hz) level. The advantage of larger diaphragms is, besides better efficiency, we cut excursion to half:

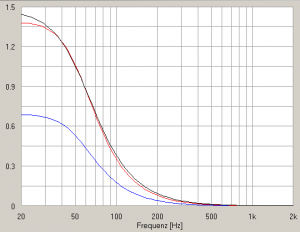
What is the advantage of reduced woofer excursion?

Simply: reduced distortion. A typical modern 8 inch woofer in a sealed 40 liter cabinet as simulated here produces > 1 percent distortion at normal listening levels. If you turn up the volume, it easily raises above 10 percent – quite a lot compared to below 0.1 percent of modern amplifiers!
A larger woofer operates at lower excursion and produces less distortion – but needs a larger cabinet.

Now imagine what a typical small bluetooth speaker – if at all capable to reproduce anything below 70 Hz – will do if you turn up the volume. Most such systems have woofer diameters below 5 inch. Not only does the transducer operate with huge distortion, but the internal amplifier will also run out of steam because of the very low transducer efficiency. Producing even more distortion.